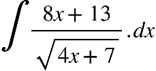Interesting and tricky integrations Part 2

 Introduction 

In this article we will learn some interesting integrations of good level.  In most of integrations you have to search that whether a derivative of any functions is existing the given question or not That is method of substitution

What is integration by substitution?

If g(x) is a continuous differentiable function, Then to evaluate the integrals of the form 

Then we can substitute g(x) = t and g'(x).dx = dt

The substitution reduces the integral to ∫f(t).dt

After evaluating the integral we will substitute the value of (t) to original one

So lets start  with some interesting and good level integration questions 

Que1) Evaluate 

Que2) Evaluate 

Que3) Evaluate 

Hint = In this question you have to rearrange the factors inside the roots after that you will obtain a new quadratic equation, Then you have to solve the quadratic equation by completing the square,

The new expression will give a function which in integral of Sec inverse  

Que4) Evaluate 

Hint = In this question you have to arrange numerator like denominator by adding and subtracting 1 in numerator and taking 2 common from the resultant term

Hope you like the post share your feedbacks in comments to make post more effective 

follow the blog for good quality maths content